ELFシリーズは現在、多くの企業や研究機関、大学で活用されています。
このソフトウェアは、IEM(積分方程式法)を用いて電磁場を計算しています。
FEM(有限要素法)やBEM(境界要素法)で解析困難な場合でも簡単に解析できる場合が多数あります。
一般にIEMは電磁場を高速で高精度に解析できるポテンシャルがあります。
オーソドックスなIEMでは解の安定性に問題がありましたが、(オーソドックスなIEMの例 ≫)
弊社ではこの原因を解明して、独自の改良をほどこしました。
その結果、高速で高精度な解が得られる計算手法を確立することができました。
ELFシリーズ5.1をリリースしました(2024年11月)
⇒ DLL版が加わり、運動連成解析や最適化計算が可能になりました。
⇒ 運動連成解析の例(アルミ選別機の解析)
⇒ 無料のDEMO版をダウンロードできます。
特長
境界要素法ではないので非線形材料の計算も得意です。
ニュートン法と反復修正法が選べます。
S字型の飽和曲線も計算可能です。
複数の物体が運動する場合、物体間の空間にメッシュが不要なので、リメッシュする必要がありません。
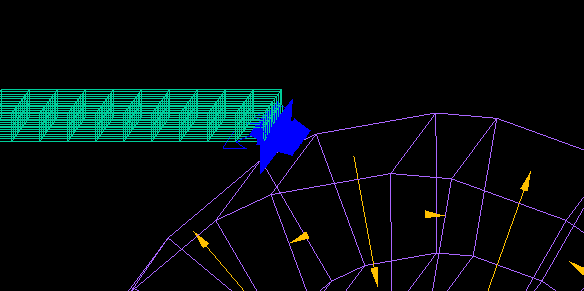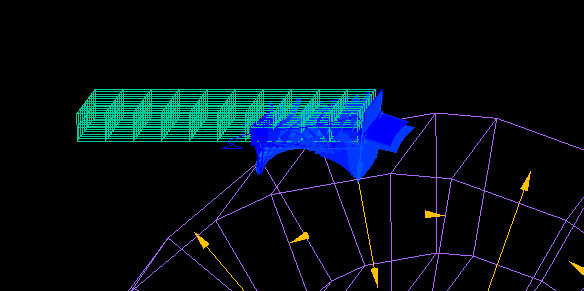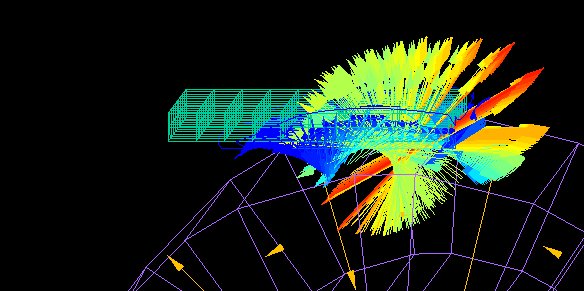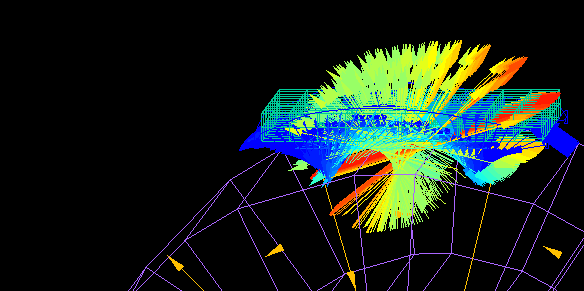


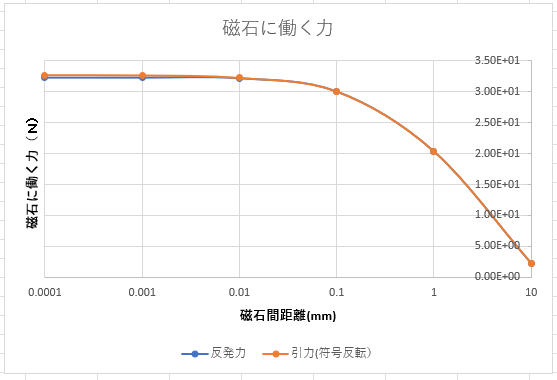
引力も反発力もごく近くに近づくまで解析式により正確に計算できます。
一辺1㎝の磁石2個を1㎝から0.1μまで近づけた時に働く力の計算です。
ギャップが狭くても引力も反発力も同じ値に収束しています。
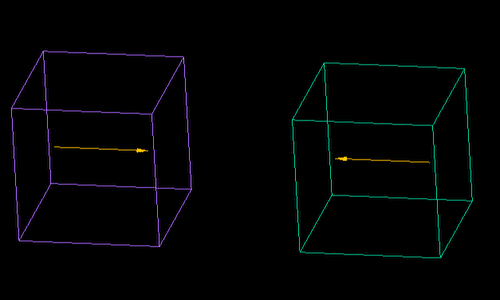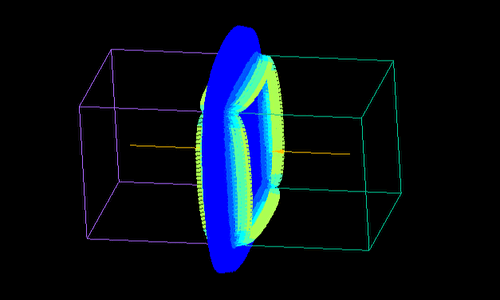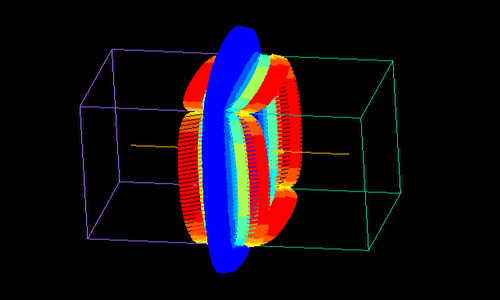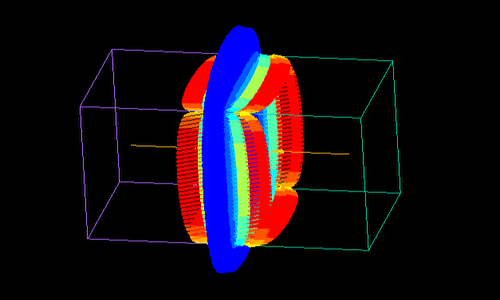
荷電粒子が磁石や電極に近接しても、解析式により精度が落ちません。
2つの部品が分離している場合はメッシュの連続性が不問なので、
メッシュサイズの極端な大小が可能です。
空間に非常に薄い磁性体がある場合は空間メッシュが不要なので簡単です。
磁石は外部から磁場が作用しても、内部の磁化の変化が少ないので極端に粗いメッシュで解析可能です。
着磁の解析も可能です。
コイル要素の分割は、空気や磁性体の分割とほぼ無関係に行えるので簡単です。
長い直線状のコイルは分割する必要がありません。
3次元解析、2次元解析、軸対称解析
静磁場解析、動磁場解析、渦電流解析、過渡解析、正弦波解析、静電場解析、荷電粒子軌道解析
磁性体、磁石、コイル、導体、磁性導体、電極、誘電体
磁場・電場、磁束密度・電束密度、渦電流、電荷密度、力、運動
誘導電流、ジュール熱、鎖交磁束、インダクタンス、荷電粒子軌道
電子顕微鏡、センサー、磁石製品、磁気シールド、モーター、リニアモーター、リレー、プランジャー、トランス
電子線ホログラフィー、スパッタリング、MEMS、磁気ヘッド、平面ブラウン管
電子銃、加速器、コンデンサ、ガイシ
無料のデモ版・使用方法
解析の手順の紹介です。
ELF/MAGIC 解析手順 ≫
ELFIN 解析手順 ≫
各ツールの使用方法やデータ作成方法です。
操作ガイド ≫
解析事例
磁場解析事例 ≫
電場解析事例 ≫
軌道解析事例 ≫
デモ版で計算できる例題 ≫
論文紹介 ≫
ユーザー ≫
解析手法
有限要素法との違い、磁気モーメント法との違い ≫
解析手法の基本的説明 ≫
従来の磁気モーメント法 ≫
従来の表面電荷法 ≫
エルフの解析手法 ≫
よくあるご質問
積分方程式法の一種です。
磁気モーメント法、表面電荷法、代用電荷法などを改良、統合した独自の手法です。
積分方程式法は電磁気学的相互作用を連立方程式で解く手法です。
磁性体やコイルをFEMと同様にメッシュ分割します。
空気の部分はメッシュ分割不要です。
磁性体の非線形BH特性はFEMと同様に扱います。
まず連立方程式を立てて解き、磁性体の磁化を確定します。
空間の磁場は磁性体の磁化から、マクスウェル方程式の積分形で計算します。
空間メッシュがないにもかかわらず、高精度な空間磁場が計算できます。
空間メッシュが不要です。
境界条件が不要です。
空間電場・空間磁場は空間で連続的に変化し、FEMのように要素境界で急に変わりません。
粗い要素でも精度よく解けます。
計算スピードがFEMより速いです。
運動の計算が空間部の再メッシュが不要なので簡単です。
積分方程式法は電磁気学的相互作用を連立方程式で解く手法です。
しかし、単純に連立方程式を立てて解くと、不自然な解が得られることが多々あります。
そのため、市販ソフトとしては成立し難い状況です。
ELFシリーズでは改良を重ね、自然な解が得られるようにしました。
単純な連立方程式の例:フランスの ESRF(欧州放射光施設)の Radiaなどがあります。
積分方程式(商用)の例 ≫
積分方程式(OSS)の例≫
有限要素法はマクスウエルの方程式の微分形を解きます。
ポテンシャルを変数としています。
空間メッシュや境界条件が必要です。
積分方程式法はマクスウエルの方程式の積分形を解きます。
電場・磁場のソースを変数としています。
空間メッシュや境界条件が不要です。
境界要素法では境界のみを分割します。
境界のみの分割なので、凹凸のある磁性体や誘電体の解析が困難であり、
磁性体の非線形BH特性の取り扱いも困難です。
表面電荷法は境界要素法に近い手法です。
ELFシリーズは表面電荷法の手法を併用し、
電位を与える電極などの安定して精度の良い部分に利用しています。
磁気モーメント法は高速に解けますが、磁束の流れが乱れることがあります。
ELFシリーズは磁気モーメント法の手法を取込み、
独自の改良を1985年,1993年,2003年,2013年に行い、
磁束の流れが乱れない自然な解が得られるようにしました。
磁場が空間に大きく漏れる装置の解析:センサーや磁気シールドなど。
3次元の解析
磁石の解析:磁石内部では磁化がほとんど変化しないので、細かい要素分割が不要です。
複雑なコイル形状:コイルから発生する磁場は、ビオサバールの法則で計算するので正確です。
物体が運動する解析:空間部の再メッシュが不要なので簡単です。
複雑な電極、誘電率の高い誘電体なども簡単に計算できます。
精密な空間電場が計算できます。
荷電粒子が飛ぶ位置に空間メッシュを作成する必要がなく、
粒子点での電場・磁場をソースからの解析式で計算するので高精度で計算できます。
また、壁などで粒子を途中で止めたりすることもできます。
磁場が空間にあまり漏れない装置の解析:モーターなど。
2次元の解析
付属のプリ・ポストのみを使って形状データの作成や結果の表示が簡単にできます。
また、NASTRAN形式やUNIVERSAL形式やFemapなどの形状データを読み込んで変換して計算することもできます。
解析事例の場合はこの要素数で十分だと考えていますが、もっと大きな問題も解けます。
また、非常に少ない要素数で有限要素法と比べて同様の精度が出ます。
CPU 10980XE 18コアのPCで解いた時間です。
15,000元(1.7GB)の密行列マトリックス 4秒
30,000元(6.7GB)の密行列マトリックス 25秒
60,000元(26.8GB)の密行列マトリックス 173秒
120,000元(107.2GB)の密行列マトリックス 23分(予想)
180,000元(241.2GB)の密行列マトリックス 78分(予想)
ELFシリーズは高度に並列化してあります。
そのため、マルチコアで計算すると、ほぼ全ての部分で高速化されます。
使用パソコンの CPU Xeon 16コア
| 並列化数 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|
| マトリックス組み立て時間(速度比) | 4.0 | 3.3 | 2.5 | 1.6 | 1.0 |
| マトリックスソルバー時間(速度比) | 10.0 | 6.5 | 3.6 | 1.9 | 1.0 |
| 空間磁場計算時間(速度比) | 11.0 | 6.5 | 3.6 | 1.9 | 1.0 |
OSは64ビットであること。(Windows11 推奨)
メモリーは32GB以上推奨。メモリーの大きさによって、解ける問題の規模が変わります。
ハードディスクは SSD を推奨
CPUは Intel社製であること。
◎ AVX512に対応したCPU
○ AVX2に対応したCPU
Pコア数が並列化数以上のPCを推奨
並列計算にEコアを参加させると計算速度が落ちます。
Eコアを除外するには、入力データで並列化数(NCPU)をPコア数以下に設定します。
ハイパースレッディングによる並列化は効果がありません。
ソルバー
磁場解析 ELF/MAGIC ≫
電場解析 ELFIN ≫
軌道解析 ELF/BEAM ≫
ツール
製品
会社情報
会社情報 ≫
デモ、セミナー ≫
お問い合わせ ≫
採用情報 ≫
a:2229553 t:61 y:352





